AVL 트리란?
AVL트리는 노드가 추가될 때, 삭제될 때 트리의 균형상태를 파악해서 스스로 그 구조를 변경하여 균형을 잡는 트리이다.
주요 특징:
- 모든 노드에서 왼쪽과 오른쪽 서브트리의 높이 차이가 최대 1
- 자동으로 균형을 유지하여 항상 O(log n) 시간 복잡도 보장
균형 인수 (Balance Factor)
AVL 트리의 핵심은 '균형 인수(밸런스 팩터)'다.
균형 인수 = 왼쪽 서브트리의 높이 - 오른쪽 서브트리의 높이
- 이 값은 항상 -1, 0, 1 중 하나여야 한다.
- 이 범위를 벗어나면 재조정(rebalancing)을 해야한다.
AVL 트리 연산
1. 검색 (Search)
일반 이진 탐색 트리와 동일한 방식으로 수행된다.
2. 삽입 (Insertion)
- 일반적인 BST 삽입 수행
- 삽입 경로를 따라 올라가며 균형 인수 업데이트
- 불균형 발생 시 회전으로 재조정
3. 삭제 (Deletion)
- 일반적인 BST 삭제 수행
- 삭제 경로를 따라 올라가며 균형 인수 업데이트
- 불균형 발생 시 회전으로 재조정
회전 연산
AVL 트리는 4가지 회전 연산을 사용한다
단일 왼쪽 회전 (LL rotation)

단일 오른쪽 회전 (RR rotation)

왼쪽-오른쪽 회전 (LR rotation)

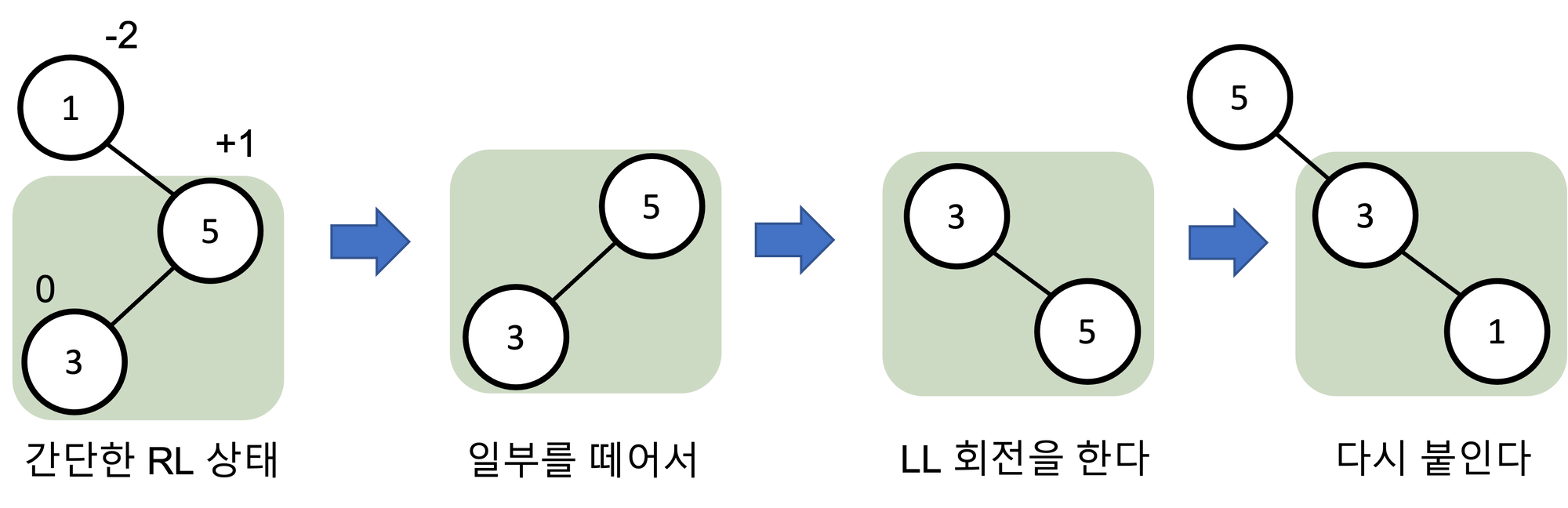
오른쪽-왼쪽 회전 (RL rotation)
AVL 트리의 장단점
장점:
- 모든 연산이 O(log n) 시간 복잡도 보장
- 완벽한 균형으로 최악의 경우에도 효율적
단점:
- 잦은 재조정으로 삽입/삭제 시 오버헤드 발생 가능
- 추가 공간 필요 (높이 정보 저장)
실제 응용
AVL 트리는 다음과 같은 상황에서 유용하다:
- 데이터베이스 인덱싱
- 메모리 할당 시스템
- 검색 빈도가 높은 파일 시스템
결론
AVL 트리는 균형 잡힌 트리 구조를 통해 효율적인 연산을 보장한다. 특히 검색 작업이 빈번한 경우에 유용하다.
'자료구조' 카테고리의 다른 글
| [자료구조] Set과 Map 근데 이제 해시와 트리를 곁들인 (1) | 2024.10.08 |
|---|---|
| [자료구조] 트리(Tree) 시리즈 5: 레드-블랙 트리(RB-Tree)란? (1) | 2024.08.04 |
| [자료구조] 트리(Tree) 시리즈 3: 이진 탐색 트리(Binary Search Tree)란? (0) | 2024.08.04 |
| [자료구조] 트리(Tree) 시리즈 2: 이진 트리(Binary Tree)란? (0) | 2024.08.04 |
| [자료구조] 트리(Tree) 시리즈 1: 트리(Tree)란? (1) | 2024.08.04 |